A second dynamic population invasion study from reactive telegraph equation and boundary element formulation – a numerical assay about tumour growth in vitro
DOI:
https://doi.org/10.20873/jbb.uft.cemaf.v10n2.pettresKeywords:
boundary element method, reactive-telegraph equation with generation, beginning and reproduction of cancer cells, sufficient condition of the solution positivity, tumour growthAbstract
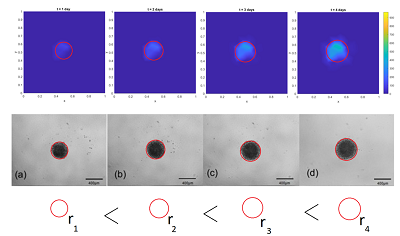
This paper is a continuation of a study already carried out on the use of the reactive-telegraph equation to analyse problems of population dynamics based on a formulation of the boundary element method (BEM). In this paper, the numerical model simulates the evolution of a tumour as a problem of population density of cancer cells from different reactive terms coupled to the reactive-telegraph equation to describe the growth and distribution of the population, similar to the two-dimensional in vitro tumour growth experiment. The mathematical model developed is called D-BEM, uses a time independent fundamental solution and the finite difference method is combined with BEM to approximate the time derivative terms and the Gaussian quadrature is used to calculate the domain integrals. The solution of the system nonlinear of equations is based on the Gaussian elimination method and the stability of the proposed formulation was verified. As the telegraph equation has a wave behaviour, a phase change phenomenon that can lead to the appearance of negative population density may occur, an algorithm was developed to guarantee the solution's positivity. Important results were obtained and demonstrate the effect of the delay parameter on tumour growth. In one of the tested cases, the results indicated an oscillatory behaviour in the tumour growth when the delay parameter assumed increasing values. The results of numerical simulations that sought to represent tumour growth, as well as the entire formulation of the boundary elements are presented below.
References
Alharbi W, Petrovskii S. Critical domain problem for the reaction–telegraph equation model of population dynamics. Mathematics, v.6, n.4, p.6–59, 2018. https://doi.org/10.3390/math6040059
Aviv-Sharon E, Aharoni A. Generalized logistic growth mod-eling of the COVID-19 pandemic in Asia. Infectious Dis-ease Modelling, v.5, p.502-509, 2020. https://doi.org/10.1016/j.idm.2020.07.003
Bacaer N. Verhulst and the logistic equation (1838), A Short History of Mathematical Population Dynamics. Springer, London, p.35-39, 2011. https://doi.org/10.1007/978-0-85729-115-8
Burkowski FJ. A computer simulation of the growth of a tumour in vitro. Computer Programs in Biomedicine, v.7, n.3, p.203-210, 1977. https://doi.org/10.1016/0010-468X(77)90028-9
Byrne HM, Chaplain MAJ. Growth of nonnecrotic tumors in the presence and absence of inhibitors. Mathematical Biosci-ences, v.130, n.2, p.151-182, 1995. https://doi.org/10.1016/0025-5564(94)00117-3
Cattaneo C. Sur uneforme de l’equation de la chaleur eliminant le paradoxed’une propagation instantanee. Comptes Rendus de l'Académiedes Sciences, v.247, p.431-433, 1958.
Chandrasekharaiah DS. Hyperbolic thermoelasticity: a review of recent literature. Applied Mechanics Reviews, v.51, n.12, p.705-729, 1998. https://doi.org/10.1115/1.3098984
Chiu SN, Stoyan D, Kendall WS, Mecke J. Stochastic geome-try and its applications. John Wiley & Sons, 2013. https://doi.org/10.1002/bimj.4710390510
Cirilo ER, Petrovskii S, Romeiro N, Natti P. Investigation into the Critical Domain Problemfor the Reaction-telegraph equa-tion Using Advanced Numerical Algorithms. International Journal of Applied and Computational Mathematics, v.5, n.54, 2019. https://doi.org/10.1007/s40819-019-0633-z
Fort J, Méndez V. Wavefronts in time-delayed reaction-diffusion systems. Theory and Comparison to Experiment. Reports on Progress in Physics, v. 65, p. 895, 2002.
Forys U, Marciniak-Czochra A. Logistic equations in tumour growth modelling. International Journal of Applied Mathe-matics and Computer Science, v.13, n.3, p.317-325, 2003.
Friedl P, Wolf, A. Tumor cell invasion and migration: diversi-ty and escape mechanisms. Nature Reviews Cancer, v.3, n.5, p.362–374, 2003. https://doi.org/10.1038/nrc1075
Gatenby RA, Vincent TL. Application of quantitative models from population biology and evolutionary game theory to tumour therapeutic strategies. American Association for Cancer Research, v.2, n.9, p.919-927, 2003.
Godoi PHV. Mathematical modeling of two-dimensional biological invasion via telegraph equation. Master's Thesis in Applied and Computational Mathematics, State Universi-ty of Londrina, Londrina, 2021.
Hillen T, Gatenby R, Hinow P. Partial Differential Equations in Cancer Modelling. Banff International Research Station for mathematiclal Innovation and Discovery. Workshopin February, p.2-6, 2015.
Holmes EE. Are Diffusion Models Too Simple? A Compari-son with Telegraph Models of Invasion. American Natural-ist, v.142, n.5, p.779-795, 1993.
Jiang C, Cui C, Li L, Shao Y. The anomalous diffusion of a tumor invading with different surrounding tissues. PLoS One, v.9, n.10, 2014. https://doi.org/10.1371/journal.pone.0109784
Johnson KE, Howard G, Mo W, Strasser MK, Lima EABF, Huang S, Brock A. Cancer cell population growth kinetics at low densities deviate from the exponential growth model and suggest an Allee effect. PLoS Biology, v.17 n.8, e3000399, 2019.https://doi.org/10.1371/journal.pbio.3000399
Katt ME, Placone AL, Wong AD, Xu ZS, Searson PC. In Vitro Tumour Models: Advantages, Disadvantages, Varia-bles, and Selecting the Right Platform. Frontiers in bioengi-neering and biotechnology, v.4, n.12, 2016. https://doi.org/10.3389/fbioe.2016.00012
Kerbel RS. Tumour angiogenesis: past, present and the near future. Carcinogenesis, v.21, n.3, p.505-515, 2000. https://doi.org/10.1093/carcin/21.3.505
Konukoglu E, Clatz O, Bondiau PY, Delignette H, Ayache N. Extrapolation glioma invasion margin in brain magnetic res-onance images: Suggesting new irradiation margins. Medi-cal Image Analysis, v.14, n.2, p.111-125, 2010. https://doi.org/10.1016/j.media.2009.11.005
Lowengrub JS, Frieboes HB, Jin F, Chuang YL, Li X, Mack-lin P, Wise SM, Cristini V. Nonlinear modelling of cancer: bridging the gap between cells and tumours. Nonlinearity, v.23, n.1, 2010. https://doi:10.1088/0951-7715/23/1/r01
Ludwig CU, Durie BG, Salmon SE, Moon TE. Tumor growth stimulation in vitro by interferons. European Journal of Cancer and Clinical Oncology, v.19, n.11, p.1625-32, 1983. https://doi.org/10.1016/0277-5379(83)90095-0
Lurie SA, Belov PA. On the nature of the relaxation time, the Maxwell–Cattaneo and Fourier law in the thermodynamics of a continuous medium, and the scale effects in thermal conductivity. Continuum Mechanics and Thermodynamics, v.32, p.709-728, 2020. https://doi.org/10.1007/s00161-018-0718-7
Mahooti, M. Gaussian Elimina-tion(https://www.mathworks.com/matlabcentral/fileexchange/73485-gaussian-elimination), MATLAB Central File Ex-change. Retrieved July 5, 2020.
Malinzi J. A mathematical model for oncolytic virus spread using the telegraph equation. Communications in Nonlinear Science and Numerical Simulation, v.102, p.1-16, 2021. https://doi.org/10.1016/j.cnsns.2021.105944
Maxwell JC. On the Dynamical Theory of Gases. The Philo-sophical Transactions of the Royal Society, v.157, n.49, p.49-88, 1867.
Méndez V, Fedotov S, Horsthemke W. Reactions and transport: diffusion, inertia, and subdiffusion.In: Reaction-Transport Systems. Springer Series in Synergetics. Spring-er, Berlin, p.33-54, 2010. https://doi.org/10.1007/978-3-642-11443-4_2
Michelson S, Glicksman SA, Leith JT. Growth in solid heter-ogeneous human colon adenocarcinomas: comparison of simple logistical models. Cell Proliferation, v.20, p.343-355, 1987.
https://doi.org/10.1111/j.1365-2184.1987.tb01316.x
Mittal RC, Dahiya S. Numerical simulation on hyperbolic diffusion equations using modified cubic B-spline differen-tial quadrature methods. Computers & Mathematics with Applications, v.70, n.5, p.737-749, 2015. https://doi.org/10.1016/j.camwa.2015.04.022
Morton KW, Mayers DF. Numerical Solutions of Partial Differential Equations. Cambridge University Press, New York, 1994. https://doi.org/10.1002/zamm.19950750904
Oliveira TF. Mathematical modeling and numeric analysis of relaxation time for reactive-diffusive-telegraph equation. 2020. Master's Dissertation in Applied and Computational Mathematics - State University of Londrina, Londrina, Bra-zil.
Onsager L. Reciprocal relations in irreversible processes. Physical Review journals, v.37, 119p., 1931. https://doi.org/10.1103/PhysRev.37.405
Painter KJ, Hillen T. Mathematical modelling of glioma growth: The use of Diffusion Tensor Imaging (DTI) data to predict the anisotropic pathways of cancer invasion. Journal of Theoretical Biology, v.323, n.21, p.25-39, 2013. https://doi.org/10.1016/j.jtbi.2013.01.014
Pettres R, Lacerda LA, Carrer JAM. A boundary element formulation for the heat equation with dissipative and heat generation terms. Engineering Analysis with Boundary El-ements, v.51, p.191-198, 2015. https://doi.org/10.1016/j.enganabound.2014.11.005
Pettres R. A first dynamic population invasion study from reactive-telegraph equation and boundary element formula-tion. Engineering Analysis with Boundary Elements, v.122, p.214-231, 2021. https://doi.org/10.1016/j.enganabound.2020.11.002
Pettres R. An introductory course on the boundary element method. v.1, p.150-153, 2020.
Preziosi L. Cancer Modelling and Simulation. Chapman Hall/CRC Press, 421 p. 2003.
Richards FJ. A flexible growth function for empirical use. Journal of Experimental Botany, v.10, n.2, p.290-301, 1959.
Sadhukhan S, Basu SK. Avascular tumour growth models based on anomalous diffusion. Journal of Biological Phys-ics, v.46, p.67-94, 2020. https://doi.org/10.1007/s10867-020-09541-w
Schwarzwälder MC. Non-Fourier Heat Conduction. The Maxwell-Cattaneo Equations. Department: Matemàtica Aplicada I Academic, Master's Degree Thesis in Science in Advanced Mathematics and Mathematical Engineering. 2015. 81p. Universitat Politècnica de Catalunya Facultat de Matemàtiquesi Estadística.
Spratt JS, Meyer JS, Spratt JA. Rates of growth of human neoplasms: part II. Journal of Surgical Oncology, v.61, p.68-73, 1996. https://doi.org/10.1002/1096-9098(199601)61:1<68::AID-JSO2930610102>3.0.CO;2-E
Sutherland RM, Durand RE. Hypoxic cells in an in vitro turnout model. International Journal of Radiation Biology and Related Studies in Physics, Chemistry and Medicine, v.23, n.3, p.235-246, 1973. https://doi.org/10.1080/09553007314550261
Swanson KR, Alvord Jr EC, Murray JD. A quantitative model for differential motility of gliomas in grey and white matter. Cell Proliferation, v.33, p.317-329, 2000. https://doi.org/10.1046/j.1365-2184.2000.00177.x
Swanson KR, Bridge C, Murray JD, JR Alvord EC. Virtual and real brain tumours: using mathematical modeling to quantify glioma growth and invasion. Journal of the Neuro-logical Sciences, v.216, n.1, p.1-10, 2003. https://doi.org/10.1016/j.jns.2003.06.001
Swanson KR. Mathematical modeling of the growth and con-trol of tumors. 1999. Ph.D thesis, University of Washing-ton.
Tao Y, Guo Q. Simulation of a model of tumors with virus-therapy. International Series of Numerical Mathematics, v.154, p.435-444, 2006.
Tilles PFC, Petrovskii SV. On the Consistency of the Reac-tion-Telegraph Process Within Finite Domains. Journal of Statistical Physics, v.177, p.569–587, 2019. https://doi.org/10.1007/s10955-019-02379-0
Vaghi C, Rodallec A, Fanciullino R, Ciccolini J, Mochel JPM, Mastri M, Poignard C, Ebos J, Benzekry S. A reduced Gompertz model for predicting tumor age using a population approach. BioRxiv, p.670869, 2019. https://doi.org/10.1101/670869
Varalta N, Gomes AV, Camargo RF. A prelude to the frac-tional calculus applied to tumour dynamic. Tema, v.15, n.2, p.211-221, 2014. https://doi.org/10.5540/tema.2014.015.02.0211
Vernotte P. Les paradoxes de lathéorie continue de l'équation de lachaleur. Comptes Rendus de l'Académiedes Sciences, v.246, n.22, p.3154-3155, 1958.
Ward JP, King JR. Mathematical modelling of avascular-tumour growth. IMA Journal of Mathematics Applied in Medicine and Biology, v.14, n.1, p.39-69, 1997. https://doi.org/10.1093/imammb/14.1.39
Wrobel LC. Potential and Viscous Flow Problems Using the Boundary Element Method. 1981. U.K. Ph.D. Thesis, Uni-versity of Southampton.
Yorke ED, Fuks Z, Norton L, Whitmore W, Ling CC. Model-ing the Development of Metastases from Primary and Local-ly Recurrent Tumours: Comparison with a Clinical Data Base for Prostatic Cancer. Cancer Research, v.53, n.13, p.2987-2993, 1993.
Zhukovsky KV. Exact solution of Guyer–Krumhansl type heat equation by operational method. International Journal of Heat and Mass Transfer, v.96, p.132-144, 2016. https://doi.org/10.1016/j.ijheatmasstransfer.2016.01.005
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2022 Roberto Pettres, Andréia Assmann Pettres, Eliandro Rodrigues Cirilo

This work is licensed under a Creative Commons Attribution 4.0 International License.
Copyright (c) 2024 - Journal of Biotechnology and Biodiversity

This work is licensed under a Creative Commons Attribution 4.0 International License.
Authors who publish with this journal agree to the following terms:
Authors retain copyright and grant the journal right of first publication with the work simultaneously licensed under a Creative Commons Attribution License (CC BY 4.0 at http://creativecommons.org/licenses/by/4.0/) that allows others to share the work with an acknowledgement of the work's authorship and initial publication in this journal.
Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the journal's published version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgement of its initial publication in this journal.
Authors are permitted and encouraged to post their work online (e.g. in institutional repositories or on their website) prior to and during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (Available at The Effect of Open Access, at http://opcit.eprints.org/oacitation-biblio.html).


